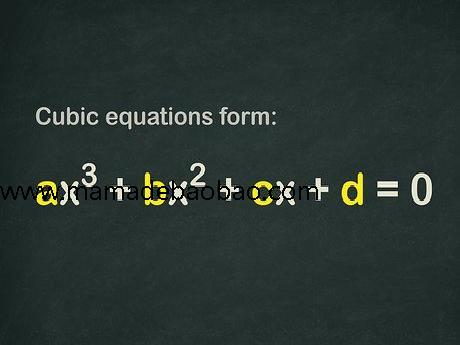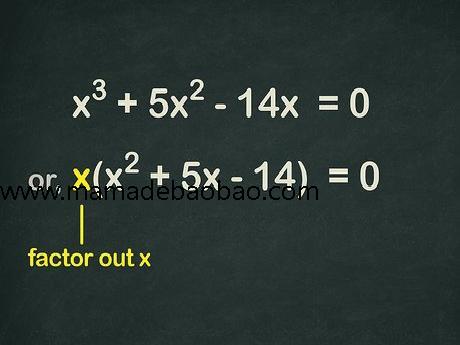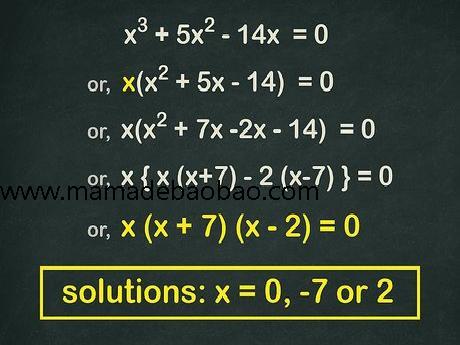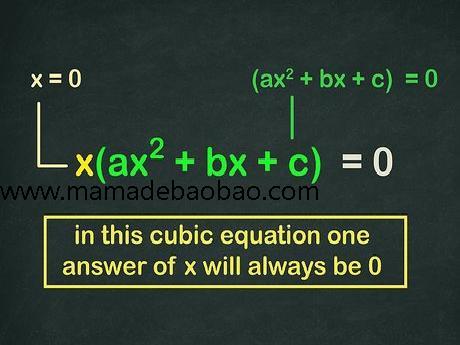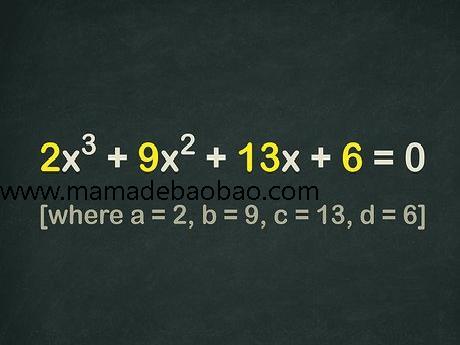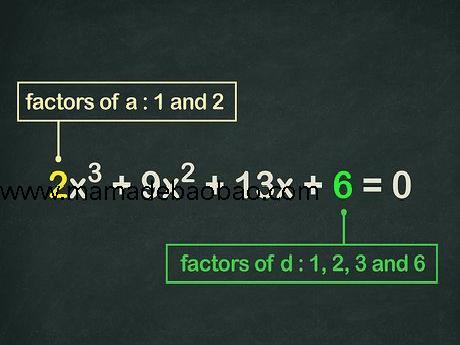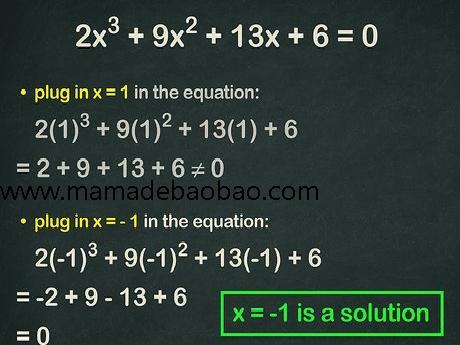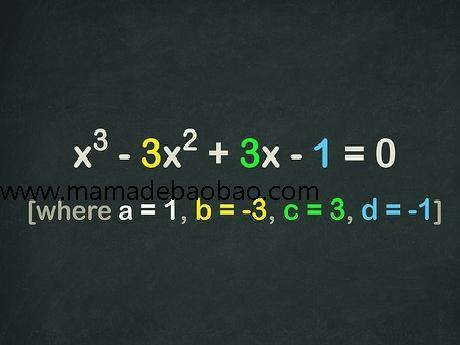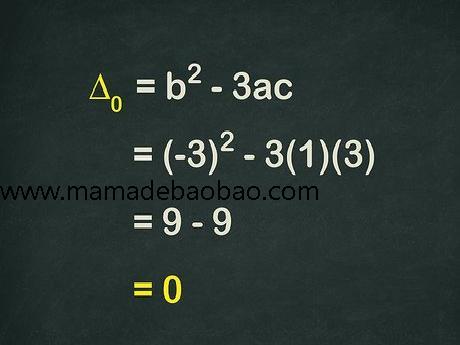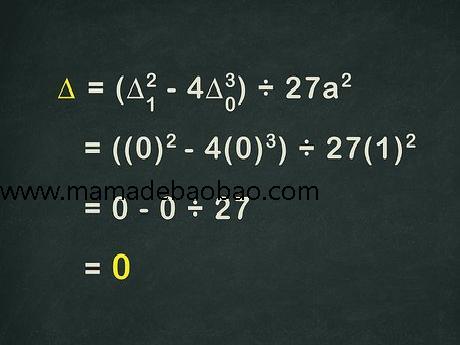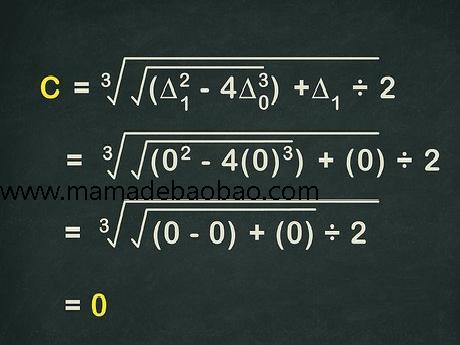3种方法来解三次方程（解不含常数项的三次方程）

如何解三次方程. 三次方程的最高次数为3次，它有3个解，或者说3个根，方程本身的形式是ax^3+bx^2+cx+d=0。虽然三次方程有些令人望而生畏，并且的确不好解，但在具备大量基础知识的前提下，只要使用正确的方法，即使是最棘手的三次方程问题也可以顺利求解。三次方程的解法有很多种，你可以尝试使用二次公式、求整数解或确定判别式方法。

方法1：解不含常数项的三次方程

1，检查三次方程，看是否包含常数项d{\displaystyle d}。三次方程的形式为ax3+bx2+cx+d=0{\displaystyle ax^{3}+bx^{2}+cx+d=0}。但是，唯一必要的关键项是x3{\displaystyle x^{3}}，这意味着三次方程中未必会出现其他项。 如果方程中包含常数项d{\displaystyle d}，那么你就必须使用其它解法。 如果a=0{\displaystyle a=0}，那么这个方程就不是三次方程。

2，提取方程的公因式x{\displaystyle x}。由于方程没有常数项，所以其中各项都包含变量x{\displaystyle x}。也就是说，可以提取方程的公因式x{\displaystyle x}来简化方程。这样做之后，可以将方程重写为x(ax2+bx+c){\displaystyle x(ax^{2}+bx+c)}。 例如，假设我们一开始要解的方程是3x3−2x2+14x=0{\displaystyle 3x^{3}-2x^{2}+14x=0}。 提取方程的公因式x{\displaystyle x}，得到x(3x2−2x+14)=0{\displaystyle x(3x^{2}-2x+14)=0}。

3，如果可能，将得到的二次方程因式分解。很多情况下，提取公因式x{\displaystyle x}后得到的二次方程ax2+bx+c{\displaystyle ax^{2}+bx+c}都能被因式分解。例如，如果要解x3+5x2−14x=0{\displaystyle x^{3}+5x^{2}-14x=0}，你可以： 提取公因式x{\displaystyle x}：x(x2+5x−14)=0{\displaystyle x(x^{2}+5x-14)=0} 将括号内的二次方程因式分解：x(x+7)(x−2)=0{\displaystyle x(x+7)(x-2)=0} 设各因式等于0{\displaystyle 0}。得到方程的解x=0,x=−7,x=2{\displaystyle x=0,x=-7,x=2}。

4，如果无法手动对括号内的部分进行因式分解，可使用二次公式求解。你可以将a{\displaystyle a}、b{\displaystyle b}、c{\displaystyle c}的值代入二次公式(−b±b2−4ac2a{\displaystyle {\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}})中，算出使二次方程等于0的x值。使用这种方法可以求出三次方程的两个解。 示例中，将a{\displaystyle a}、b{\displaystyle b}和c{\displaystyle c}的值3{\displaystyle 3}、−2{\displaystyle -2}和14{\displaystyle 14}分别代入到以下二次公式： −b±b2−4ac2a{\displaystyle {\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}} −(−2)±((−2)2−4(3)(14)2(3){\displaystyle {\frac {-(-2)\pm {\sqrt {((-2)^{2}-4(3)(14)}}}{2(3)}}} 2±4−(12)(14)6{\displaystyle {\frac {2\pm {\sqrt {4-(12)(14)}}}{6}}} 2±(4−1686{\displaystyle {\frac {2\pm {\sqrt {(4-168}}}{6}}} 2±−1646{\displaystyle {\frac {2\pm {\sqrt {-164}}}{6}}} 解1: 2+−1646{\displaystyle {\frac {2+{\sqrt {-164}}}{6}}} 2+12.8i6{\displaystyle {\frac {2+12.8i}{6}}} 解2: 2−12.8i6{\displaystyle {\frac {2-12.8i}{6}}}

5，零和二次方程的解就是三次方程的解。二次方程有两个解，而三次方程有三个。你已经求出其中的两个解，即你为括号中"二次"部分求出的解。对于可以用"因式分解"方法求解的方程，第三个解一定为0{\displaystyle 0}。 将方程分解为包含两个因式的形式x(ax2+bx+c)=0{\displaystyle x(ax^{2}+bx+c)=0}，左边的因式是变量x{\displaystyle x}，右边的因式是括号内的二次方程。如果任一因式等于0{\displaystyle 0}，则整个方程等于0{\displaystyle 0}。 因此，使括号内的二次因式等于0{\displaystyle 0}的两个解是三次方程的解，而使左边因式等于0{\displaystyle 0}的0{\displaystyle 0}本身，也是三次方程的解。

方法2：使用因数表求整数解

1，确保三次方程有一个d{\displaystyle d}值不等于零的常数项。如果形式为ax3+bx2+cx+d=0{\displaystyle ax^{3}+bx^{2}+cx+d=0}的方程拥有一个不等于零的d{\displaystyle d}值，那就无法将它因式分解为二次方程。但是不用担心，你还可以使用其他方法，比如下文中介绍的方法。 以方程2x3+9x2+13x=−6{\displaystyle 2x^{3}+9x^{2}+13x=-6}为例。这个方程中，要让等号的右边等于0{\displaystyle 0}，你需要两边都加6{\displaystyle 6}。 得到新的方程2x3+9x2+13x+6=0{\displaystyle 2x^{3}+9x^{2}+13x+6=0}。由于d=6{\displaystyle d=6}，你无法使用二次方程方法。

2，找出a{\displaystyle a}和d{\displaystyle d}的因数。要解三次方程，我们需要先关注x3{\displaystyle x^{3}}项的系数a{\displaystyle a}以及方程最后的常数项d{\displaystyle d}，找出它们各自的因数。记住，如果两个数字相乘得到另一个数，那么这两个数就是乘积的因数。 例如，由于你可以用6×1{\displaystyle 6\times 1}和2×3{\displaystyle 2\times 3}得到6，所以1、2、3、6就是6的因数。 例题中，a=2{\displaystyle a=2}，而d=6{\displaystyle d=6}。2的因数是1和2。6的因数是1、2、3、6。

3，用a{\displaystyle a}的因数除以d{\displaystyle d}的因数。将a{\displaystyle a}的各因数除以d{\displaystyle d}的各因数所得的值罗列出来。这样做通常会得到许多分数和几个整数。三次方程的整数解要么是其中的一个整数，要么是其中一个整数的相反数。 例题中，用a{\displaystyle a}的因数1和2除以d{\displaystyle d}的因数1、2、3、6，得到：1{\displaystyle 1}，12{\displaystyle {\frac {1}{2}}}，13{\displaystyle {\frac {1}{3}}}，16{\displaystyle {\frac {1}{6}}}，2{\displaystyle 2}和23{\displaystyle {\frac {2}{3}}}。然后，我们将各数字的相反数加入进去，使之更加完整：1{\displaystyle 1}，−1{\displaystyle -1}，12{\displaystyle {\frac {1}{2}}}，−12{\displaystyle -{\frac {1}{2}}}，13{\displaystyle {\frac {1}{3}}}，−13{\displaystyle -{\frac {1}{3}}}，16{\displaystyle {\frac {1}{6}}}，−16{\displaystyle -{\frac {1}{6}}}，2{\displaystyle 2}，−2{\displaystyle -2}，23{\displaystyle {\frac {2}{3}}}和−23{\displaystyle -{\frac {2}{3}}}。三次方程的整数解就在其中。

4，手动代入整数，这种方法较为简单，但可能会比较费时。得到相除的结果后，你可以迅速将整数手动代入，看哪些能让三次方程等于0{\displaystyle 0}，进而求出方程的解。例如，如果将1{\displaystyle 1}代入方程，可以得到： 2(1)3+9(1)2+13(1)+6{\displaystyle 2(1)^{3}+9(1)^{2}+13(1)+6}，即2+9+13+6{\displaystyle 2+9+13+6}，结果不等于0{\displaystyle 0}。因此，使用得到的下一个值。 如果将−1{\displaystyle -1}代入方程，得到(−2)+9+(−13)+6{\displaystyle (-2)+9+(-13)+6}，结果等于0{\displaystyle 0}。这意味着−1{\displaystyle -1}是方程的一个整数解。

5，使用更复杂，但可能更快速的综合除法。如果你不想花时间一个一个地去代入所有的值，不妨尝试一下更快捷的方法，也就是所谓的综合除法。总的来说，你应该使用综合除法，用得到的整数值除以a{\displaystyle a}、b{\displaystyle b}、c{\displaystyle c}和d{\displaystyle d}。如果得到余数0{\displaystyle 0}，那么这个值就是三次方程的解。 综合除法是一个复杂的主题，超出了本文论述的范围。以下的例子示范了如何用综合除法求三次方程的解： -1 | 2 9 13 6 __| -2-7-6 __| 2 7 6 0 由于得到的最终余数为0{\displaystyle 0}，由此可知，−1{\displaystyle -1}是三次方程的一个整数解。

方法3：使用判别式方法

1，写下a{\displaystyle a}、b{\displaystyle b}、c{\displaystyle c}和d{\displaystyle d}的值。本方法会大量用到方程各项的系数。开始前，记下a{\displaystyle a}、b{\displaystyle b}、c{\displaystyle c}和d{\displaystyle d}的值，免得之后混淆。 对于例题x3−3x2+3x−1{\displaystyle x^{3}-3x^{2}+3x-1}，写下a=1{\displaystyle a=1}、b=−3{\displaystyle b=-3}、c=3{\displaystyle c=3}和d=−1{\displaystyle d=-1}。注意，如果有x{\displaystyle x}变量前没有系数，这代表它的系数为1{\displaystyle 1}。

2，使用正确的公式计算判别式零。用判别式方法求三次方程的解会用到十分复杂的数学原理，但如果严格遵循方法流程，你会发现，它在解令其他方法束手无策的三次方程方面十分实用。首先，将适当的值代入到公式Δ0=b2−3ac{\displaystyle \Delta _{0}=b^{2}-3ac}中，求出第一个重要数值，即判别式零Δ0{\displaystyle \Delta _{0}}。 判别式是一个数字，可以为我们提供关于多项式根的信息。你可能已经知道二次判别式是(b2−4ac{\displaystyle b^{2}-4ac})。 例题中的计算过程如下： b2−3ac{\displaystyle b^{2}-3ac} (−3)2−3(1)(3){\displaystyle (-3)^{2}-3(1)(3)} 9−3(1)(3){\displaystyle 9-3(1)(3)} 9−9=0=Δ0{\displaystyle 9-9=0=\Delta _{0}}

3，然后，计算Δ1=2b3−9abc+27a2d{\displaystyle \Delta _{1}=2b^{3}-9abc+27a^{2}d}。你需要的下一个重要数值是判别式1{\displaystyle 1}，即Δ1{\displaystyle \Delta _{1}}，它的计算过程会稍微复杂一点，但方法与Δ0{\displaystyle \Delta _{0}}基本相同。将适当的值代入到公式2b3−9abc+27a2d{\displaystyle 2b^{3}-9abc+27a^{2}d}中，得到Δ1{\displaystyle \Delta _{1}}的值。 例题中的计算过程如下： 2(−3)3−9(1)(−3)(3)+27(1)2(−1){\displaystyle 2(-3)^{3}-9(1)(-3)(3)+27(1)^{2}(-1)} 2(−27)−9(−9)+27(−1){\displaystyle 2(-27)-9(-9)+27(-1)} −54+81−27{\displaystyle -54+81-27} 81−81=0=Δ1{\displaystyle 81-81=0=\Delta _{1}}

4，计算: Δ=(Δ12−4Δ03)÷−27a2{\displaystyle \Delta =(\Delta _{1}^{2}-4\Delta _{0}^{3})\div -27a^{2}}。然后，我们会使用Δ0{\displaystyle \Delta _{0}}和Δ1{\displaystyle \Delta _{1}}的值计算三次方程的判别式。在三次方程中，如果判别式为正数，则方程有三个实数解。如果判别式等于零，则方程有一个或两个实数解，且有时两个实数解会相等。如果判别式为负数，则方程只有一个实数解。 三次方程必定有至少一个实数解，因为其函数图形必定会与X轴相交至少一次。 例题中，由于Δ0{\displaystyle \Delta _{0}}和Δ1{\displaystyle \Delta _{1}}都等于0{\displaystyle 0}，所以Δ{\displaystyle \Delta }的计算相对简单。计算过程如下： (Δ12−4Δ03)÷(−27a2){\displaystyle (\Delta _{1}^{2}-4\Delta _{0}^{3})\div (-27a^{2})} ((0)2−4(0)3)÷(−27(1)2){\displaystyle ((0)^{2}-4(0)^{3})\div (-27(1)^{2})} 0−0÷27{\displaystyle 0-0\div 27} 0=Δ{\displaystyle 0=\Delta }，所以方程有一个或两个解。

5，计算: C=3(Δ12−4Δ03+Δ1)÷2{\displaystyle C=^{3}{\sqrt {\left({\sqrt {\Delta _{1}^{2}-4\Delta _{0}^{3}}}+\Delta _{1}\right)\div 2}}}。最后一个需要计算的重要数值是C{\displaystyle C}。它能帮助我们在最后求出三个根。按照正常计算过程，根据需要代入 Δ1{\displaystyle \Delta _{1}}和Δ0{\displaystyle \Delta _{0}}。 例题中，C{\displaystyle C}的计算过程如下： 3(Δ12−4Δ03)+Δ1÷2{\displaystyle ^{3}{\sqrt {{\sqrt {(\Delta _{1}^{2}-4\Delta _{0}^{3})+\Delta _{1}}}\div 2}}} 3(02−4(0)3)+(0)÷2{\displaystyle ^{3}{\sqrt {{\sqrt {(0^{2}-4(0)^{3})+(0)}}\div 2}}} 3(0−0)+0÷2{\displaystyle ^{3}{\sqrt {{\sqrt {(0-0)+0}}\div 2}}} 0=C{\displaystyle 0=C}

6，使用变量计算三个根。三次方程的根或解可以使用公式−(b+unC+Δ0÷(unC))÷3a{\displaystyle -(b+u^{n}C+\Delta _{0}\div (u^{n}C))\div 3a}计算，其中u=(−1+−3)÷2{\displaystyle u=(-1+{\sqrt {-3}})\div 2}，而n等于1、2或3。根据需要代入数值进行计算，其中涉及到大量的数学运算，但你应该可以得到三个使方程成立的解。 你可以分别计算n等于1、2、3时公式的值，来求得例题的答案。这样得到的答案可能就是三次方程的解。你可以将答案代入到方程中，使之等于0的答案即为方程的正确解。 例如，将1代入到x3−3x2+3x−1{\displaystyle x^{3}-3x^{2}+3x-1}中，计算结果为0，所以1就是三次方程的一个解。